저번에는 중첩의 원리를 정리하면서 전류분배법칙에 대해 살짝 언급했습니다.
전압분배법칙과 전류분배법칙은 회로 문제 풀이 시간을 단축시켜줄 뿐만 아니라 원하는 값만 따로 구할 수 있다는 장점이 있습니다.
모든 노드에 값을 찾은 후 답을 찾을 필요가 없기 때문에 당연히 알아두면 좋습니다.
전압/전류분배법칙을 알아보기 전에 직/병렬 연결에 대해 정확하게 이해하고 있어야 합니다.
먼저 직렬 연결이란, 말 그래도 한 직선으로 소자가 연결되어 있습니다.
따라서 직렬 연결된 소자에 흐르는 전류는 동일하며, 전압은 다릅니다.
여러 저항이 직렬로 연결되어 있다면 단순히 저항값을 더함으로써 등가 저항을 구할 수 있습니다.
등가 저항이란, 임의로 정한 저항 소자들 묶음의 저항값과 동일한 저항값을 의미합니다.
아래와 같이 직렬로 연결된 저항 소자들이 있습니다.

직렬 연결된 저항 소자들의 등가 저항은 이런 식으로 구할 수 있습니다.
이어서 병렬 연결이란, 2줄 이상으로 소자가 연결되어 있습니다.
병렬 연결된 소자에 흐르는 전류는 다르며, 전압은 동일합니다.
병렬 연결된 저항 소자들의 등가 저항은 아래처럼 구할 수 있습니다.
(저항값은 제가 임의로 정해서 계산이 깨끗하진 않습니다.)

직렬/병렬 등가 저항을 구하는 방식이 다른 이유는 아래와 같습니다.
이전에 정리한 path를 떠올리며 이해하면 더 쉽습니다.
전류가 흐르는 길(path)가 하나로 흐르면 직렬, 나누어지면 병렬입니다.
정리!

cf. 등가 저항을 구하는 이유는 복잡한 회로를 보기 쉽게 만들기 위해서입니다.
나중에 테브난 등가회로를 배우기 전에 맛보기 정도로 생각하면 됩니다.
이제 본격적으로 전압분배법칙과 전류분배법칙에 대해 알아보자면,
전압분배법칙이란, 전압 A에 비례하는 전압 B를 정하기 위한 법칙입니다.
일반적으로 Vin은 입력 전압, 즉 전원에서 공급하는 전압이며, Vout은 출력 전압을 의미합니다.
Vout은 회로에서 제시하기 때문에 찾을 필요는 없어요.
그러나, Vin과 Vout 중 하나만 알면 다른 하나의 값을 구할 수 있어야 합니다.
아래 회로를 보고 위의 직렬/병렬 연결의 특성을 이용해 Vout 값을 구해보아요.
힌트는 옴의 법칙(V=IR)입니다.
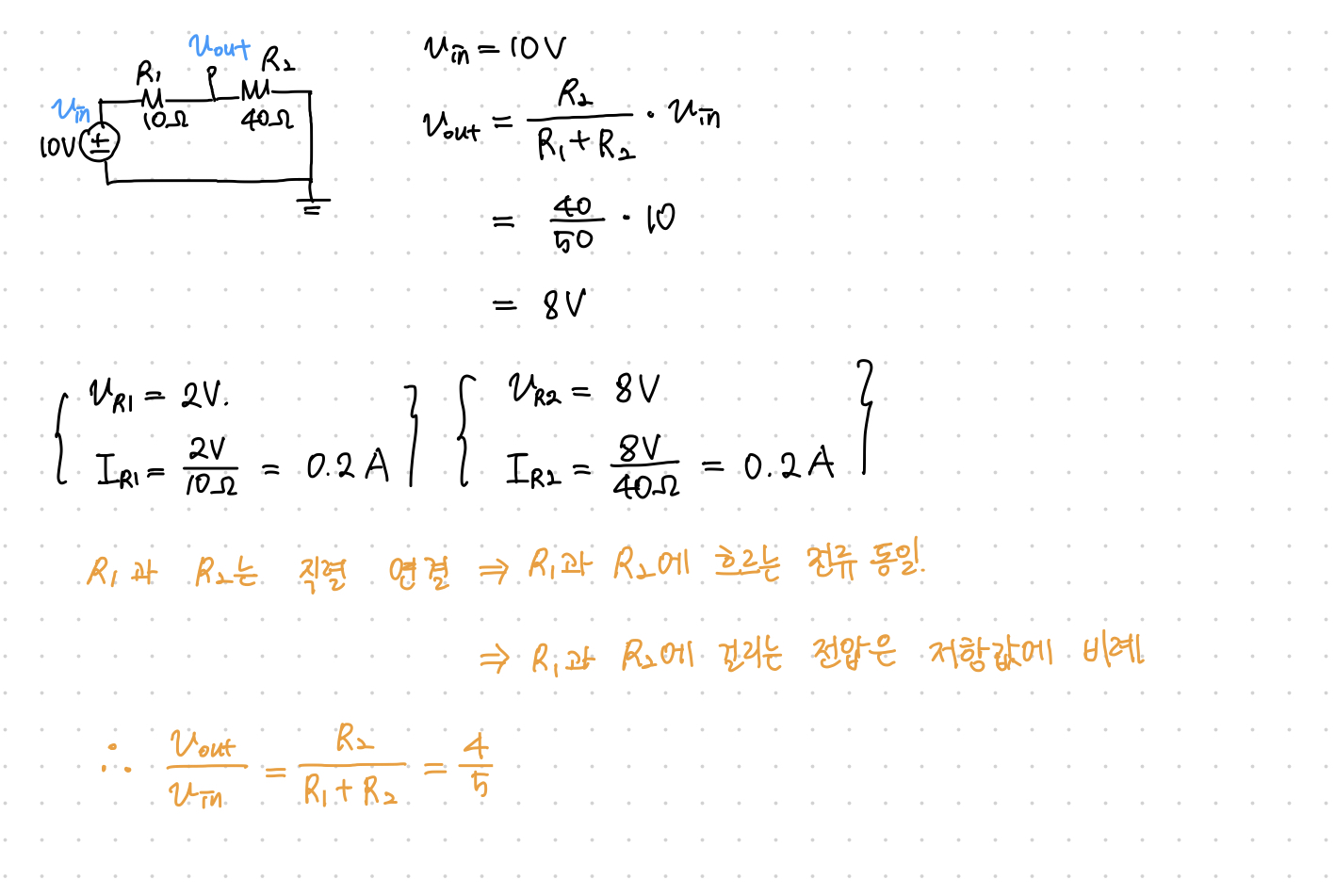
위 예제를 제대로 이해했다면, 다음 예제를 풀어보아요.

저는 아래처럼 풀었습니다.

cf는 정리한 내용은 직렬 연결 회로의 성질을 이용한 것입니다.
글이 길어져서 전류분배법칙은 다음에 정리해보겠습니다.
궁금한 점은 댓글로 남겨주세요.
'회로이론' 카테고리의 다른 글
| 회로이론 #06 직렬/병렬 연결과 전압분배법칙 & 전류분배법칙 2 (0) | 2023.08.11 |
|---|---|
| 회로이론 #05 테브난 등가 회로 (0) | 2023.07.25 |
| 회로이론#03 중첩의 원리 (0) | 2023.07.13 |
| 회로이론#02 KVL과 KCL(키르히호프 전압, 전류 법칙) (0) | 2023.07.10 |
| 회로이론#01 마디, 경로, 루프 그리고 가지 (0) | 2023.07.02 |



