이제 옴의 법칙 다음으로 유명한 키르히호프 전압 법칙과 키르히호프 전류 법칙에 대해 알아보겠습니다.
먼저 정의부터 하자면 다음과 같습니다.
1. KVL(키르히호프 전압 법칙): 폐회로에서 시작점과 끝점이 같으면 전압의 합은 0이다.
2. KCL(키르히호프 전류 법칙): 한 노드에서 들어오고 나가는 전류의 합은 0이다.
이렇게 글로만 봤을 때는 진짜 간단합니다.
하지만 막상 적용하려고 하면 전제조건을 설정하고 방향을 제대로 기억해야 하기 때문에 임의로 왼쪽은 +, 오른쪽은 -로 고정하는 편이 쉽습니다.
이후 문제에서 지정해주는 방향이 있을 경우 그에 맞춰서 부호를 결정하는게 더 편하고요.
중요한 건, 문제에서 어떤 공식으로 풀라고 제시해주지 않기 때문에 회로를 보고 어떤 공식을 적용해야 답을 구할 수 있는지 빨리 파악하는 것입니다.
연습하다보면 아, 이건 KVL이고 저건 KCL로 풀어야지하고 감이 옵니다.
팁을 드리자면 노드와 루프를 세어봤을 때, 일반적으로 노드가 적을 때는 KCL, 루프가 적을 때는 KVL로 풀이하는게 더 빠릅니다.
노드와 루프는 이전에 다루었기 때문에 자세한 설명은 아래 링크를 통해 확인해주세요.
회로이론#01 마디, 경로, 루프 그리고 가지
저번에 소자에 대해 알아봤으니 이번엔 소자와 소자 사이의 관계를 정의해보아요. 소자에 대해 아직 정리가 되지 않았다면 아래 링크로 확인할 수 있습니다. https://gamjainhell.tistory.com/entry/%ED%9A%8C
gamjainhell.tistory.com
1. KVL
아래와 같은 예시를 들어보겠습니다.

위 회로에서 루프와 노드를 구분해서 KVL, KCL 선택해서 풀이 가능하지만 이번에는 KVL로 풀어보겠습니다.

좌측 폐회로 먼저 적용해보면 아래와 같습니다.
R3, R4는 직렬로 연결되어 있기 때문에 저항값은 단순 덧셈으로 구할 수 있으며 R3+R4=Req로 묶을 수 있습니다.
이번에는 저항값을 구할 필요가 없지만 복잡한 회로 문제에서 이런 식으로 묶어서 단순화시키는 습관을 들이는 편이 좋아요.
파란색 방향은 임의로 설정했으며 앞에 설명한 대로 + ㅡ> - 방향을 기준으로 합니다.

이렇게 Req에 걸리는 전압이 32V인 걸 알 수 있습니다.
다음으로 우측 폐회로를 살펴보겠습니다.
주의할 점은 파란색 방향입니다.

좌측 회로와는 달리 Req에 걸리는 전압 방향을 고려해 (-)부호를 붙여서 KVL을 적용합니다.
우측에서 V1과 R1에 걸리는 전압 둘 다 모르기 때문에 각각의 전압값을 알 수 없지만 V1과 R1이 포함된 노드에 걸리는 전압은 구할 수 있습니다.
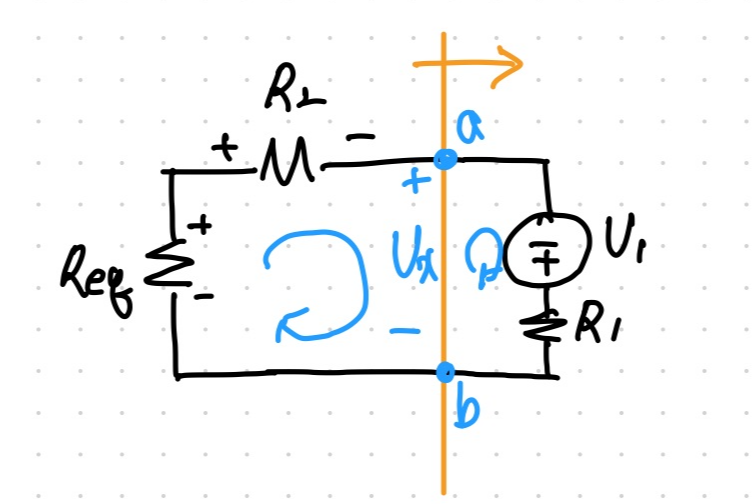
위처럼 주황색 선을 기준으로 좌측의 전압값은 알고 있으며 우측 전압값은 모르는 상태에서 Vx = a-b 노드에 걸리는 전압을 의미합니다.
따라서 Req=32V, R2에 걸리는 전압은 12V이므로 KVL을 적용하면,
-32+12+Vx=0
Vx=20V를 구할 수 있습니다.
예시처럼 폐회로가 여러 개 있을 때는 미지값이 적은 폐회로 순서대로 하나씩 KVL을 적용하면 값을 구할 수 있습니다.
2. KCL
아래와 같은 예시를 들어보겠습니다.
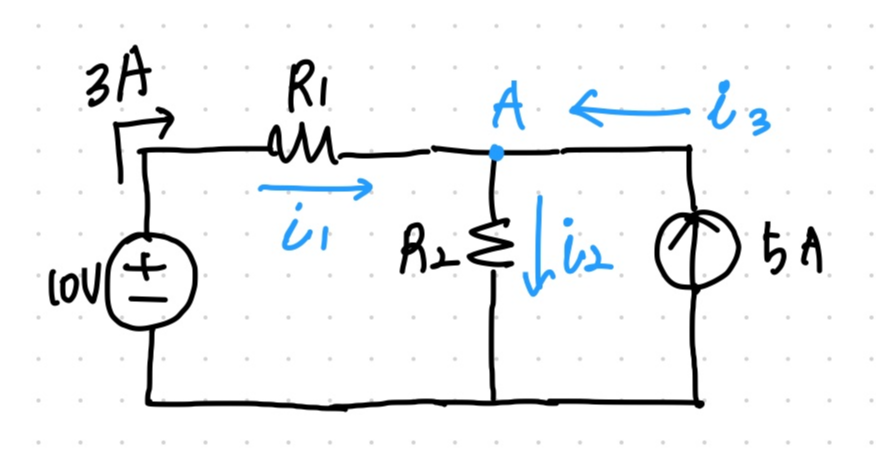
아주 간단한 회로로 가져왔습니다. 노드 A에서 들어오고 나가는 전류의 합은 0이다. (=KCL)을 적용해서 i1, i2, i3를 모두 구할 수 있습니다.
사실 전류원이 보이기 때문에 i3=5A를 바로 구할 수 있습니다.
이후 R1에 흐르는 전류가 3A로 주어졌기 때문에 i1=3A입니다.
따라서 KCL 식을 세우면 아래와 같습니다.
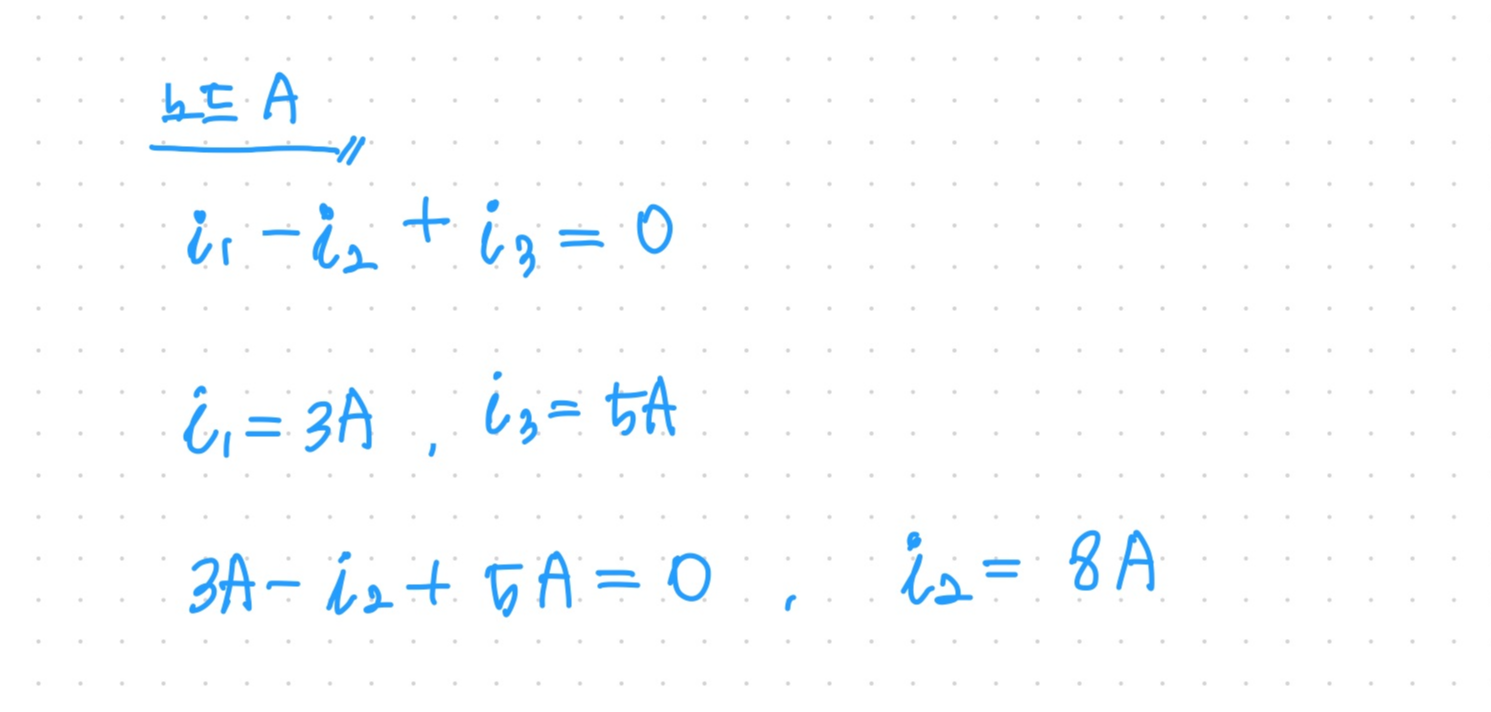
이렇게 i2=8A로 구할 수 있습니다.
마무리하면,,,
KVL과 KCL 모두 방향성이 중요하다는 점만 기억하면 적용하기 어렵지 않습니다.
이번에는 간단한 회로로 예시를 들었기 때문에 복잡한 회로에서는 어떻게 적용하는지는 추후 풀어보겠습니다.
'회로이론' 카테고리의 다른 글
| 회로이론 #05 테브난 등가 회로 (0) | 2023.07.25 |
|---|---|
| 회로이론 #04 직렬/병렬 연결과 전압분배법칙 & 전류분배법칙 1 (0) | 2023.07.24 |
| 회로이론#03 중첩의 원리 (0) | 2023.07.13 |
| 회로이론#01 마디, 경로, 루프 그리고 가지 (0) | 2023.07.02 |
| 회로이론을 시작하기 앞서,,,회로이론#00기본 소자와 단위, 옴의 법칙 (0) | 2023.06.30 |



