사실 이 포스팅을 찾아보시는 여러분은 증명 과정은 안 궁금해하시지 않을까 싶어요.
그래서 그냥 공식만 적어볼까 하다가 저 역시도 공식만 암기했다가 시험에서 폭망한 적이 있어서 조금 길게 써보려고 합니다.
처음부터 각잡고 증명할 생각은 없으니 안심하세요,,,
그냥 공식만 외우면 시험때 기억이 안나요,,,(제가 그랬어요.)
각설하고 일단 3X3 행렬식 먼저 구해보겠습니다.
이전 포스팅에서 살짝 언급했지만 행렬식을 구하는 방법은 크게 3가지 정도입니다.
2개는 정석이고 하나는 야매라고 생각하면 되구요, 우린 서술형 시험을 준비한다는 마음가짐으로 정석으로 풀어보아요.
먼저, 예시가 되는 행렬은 다음과 같습니다.

위 행렬을 A라고 합시다. 이제 det(A)를 구할 겁니다만, 기본행 연산을 통해서 가우스 - 조르단 소거법을 이용해 구해보겠습니다.
기본행 연산이란? 3가지만 기억하시면 됩니다. (행을 위에서 아래 방향으로 계산하는 것은 기본)
1) 한 행에 실수배 가능.
2) 두 행의 위치 변경 가능.
3) 한 행에 실수배한 후 다른 행에 더하기/빼기 가능.
또한 이렇게 기본행 연산을 한 번 할 때마다 나오는 행렬들은 기본행렬이라고도 합니다. 그냥 이런게 있구나, 하시면 됩니다.
이제 가우스-조르단 소거법을 정의하자면, 구하고자 하는 행렬 A 옆에 단위행렬을 붙여주는 걸 의미합니다. 기호로는 다음과 같습니다.

그리고 이걸 첨가행렬이라고 합니다.
이 상태에서 기본행 연산을 통해서 A 행렬을 단위행렬로 만들면, 단위행렬은 A의 역행렬이 됩니다.
말로는 좀 어렵죠?
먼저 1행에 -2를 곱한 후(실수배) 2행에 더합니다. <- 기본행 연산
1행은 그대로 유지되며 2행만 변합니다. 아래와 같이 변하겠네요.

왼쪽 행렬을 기본행 연산으로 단위행렬로 만들기 위해서는 1열에 (1,1)원소를 제외하고 모두 0으로 만들어줘야합니다.
따라서 이제 1행에 -7/2를 곱한 후 3행에 더합니다. -> (3,1)의 원소를 0으로 만들기 위해서입니다. <- 기본행 연산

이제 1열의 (1,1) 원소를 제외한 원소들은 0이 되었습니다. 다음으로 2열 2행의 원소만 남기고 0으로 만들어야 합니다.
저는 편의를 위해 2행을 1/7로 나눈 후 2행 2열을 제외하고 0으로 만들겠습니다. <- 기본행 연산
일단 2행에 1/7을 곱하면 다음과 같습니다.

2행에 -3/2를 곱한 후 3행에 더해줍니다. 이후에 2행에 -1을 곱한 후 1행에 더해줍니다.

이제 마지막으로 3행 3열의 원소를 1로 만들고 3열의 나머지 원소들을 0으로 만들면 역행렬을 구할 수 있습니다.

결과는 이렇게 나옵니다. 바로 우측 3X3 행렬이 A 행렬의 역행렬입니다.
다시 말해, 원래 단위 행렬이었던 I 행렬이 A 행렬의 역행렬입니다.
과정을 따라해보셨다면 4X4 행렬은 굳이 해보지 않아도 알 수 있겠죠?
게다가 역행렬을 구하는 과정은 모두 기본행 연산이기 때문에 기본행 연산 결과로 나온 행렬들을 순서대로 곱하면 A 행렬을 구할 수 있어요. (이건 지금 중요하지 않으니 넘어가겠습니다.)
가우스-조르단 행렬로 역행렬을 구하는데 걸리는 시간과 정밀함을 따지면 이걸 할 이유가 없어요.
근데 교수님이 이걸로 풀라고 하시면,,,풀어야 하기 때문에 할줄은 알아야 합니다.
공학용 계산기로 연습하고 정답을 확인해봐도 좋고 웹사이트로 역행렬 계산기를 돌려도 상관없습니다.
기본행 연산 과정과 가우스-조르단 소거법을 이해하셨다면요.
참고로, 가우스 행렬은 아래와 같이 삼각형 모양으로 원소가 있고 나머지는 0인 원소를 가진 행렬을 의미합니다. 선두가 굳이 1일 필요는 없어요,
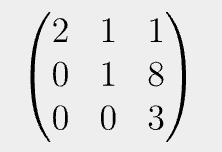
가우스-조르단 행렬은 선두가 포함되어 있는 열은 모두 0이어야 하는 행렬입니다. 예시는 아래와 같습니다.

위와 같이 선두가 포함되어 있는 열에는 선두를 제외하고 모두 0인 원소를 가져야 합니다.
이제 가우스-조르단 소거법을 다뤘으니 다음에는 수반행렬을 이용한 역행렬 구하기를 해보겠습니다.
'선형대수학' 카테고리의 다른 글
| 선형대수학#3. 단위 행렬과 거듭제곱, 곱셈의 특성 (1) | 2024.05.28 |
|---|---|
| 선형대수학 #4 3X3 행렬 수반행렬 이용해 역행렬 구하기 (0) | 2023.12.12 |
| 선형대수학 #1. 정칙/가역 행렬과 역행렬 (0) | 2023.11.05 |
| 선형대수학 #0.행렬이란, 행과 열, 사칙연산 공식 (1) | 2023.10.31 |



